446. Трапеция ABCD
с основаниями BC=2
и AD=10
такова, что в неё можно вписать окружность и около неё можно описать окружность. Определите, где находится центр описанной окружности, т. е. расположен он внутри или вне её, или же на одной из сторон трапеции ABCD
. Найдите также отношение радиусов описанной и вписанной окружностей.
Ответ. Вне; \frac{3\sqrt{14}}{5}
.
Указание. Докажите, что угол ACD
— тупой. Радиус описанной окружности найдите по формуле: R=\frac{a}{2\sin\alpha}
.
Решение. Пусть R
и r
— радиусы вписанного и описанного кругов, K
— основание перпендикуляра, опущенного из вершины C
на сторону AD
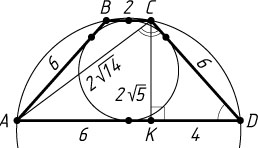
. Поскольку трапеция вписанная, то она равнобедренная. Тогда AK=6
, KD=4
, а т. к. 2\cdot CD=BC+AD
, то CD=6
. Отсюда находим, что
CK=2\sqrt{5},~AC=2\sqrt{14}.
С помощью теоремы косинусов убеждаемся, что угол \angle ACD
тупой. Поэтому центр описанного круга лежит вне трапеции. Кроме того,
\sin\angle D=\frac{CK}{CD}=\frac{\sqrt{5}}{3}.
Поэтому
R=\frac{AC}{2\sin\angle D}=\frac{3\sqrt{14}}{5},~r=\frac{1}{2}CK=\sqrt{5}.
Следовательно,
\frac{R}{r}=\frac{3\sqrt{14}}{5}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1968, вариант 1, № 1
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 1, № 1, с. 316
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.11, с. 86
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 22, с. 140
