448. На отрезке AB
, равном 2R
, как диаметре построена окружность. Вторая окружность, радиус которой равен половине радиуса первой окружности, касается её внутренним образом в точке A
. Третья окружность касается первой окружности внутренним образом, второй окружности — внешним образом, а также касается отрезка AB
. Найдите радиус третьей окружности.
Ответ. \frac{4R}{9}
.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
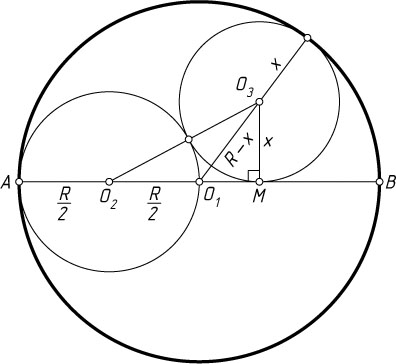
Решение. Пусть O_{1}
, O_{2}
, O_{3}
— центры первой, второй и третьей окружностей соответственно, x
— радиус третьей окружности, M
— её точка касания с отрезком AB
. Тогда
O_{1}M=\sqrt{O_{1}O_{3}^{2}-MO_{3}^{2}}=\sqrt{(R-x)^{2}-x^{2}}=\sqrt{R^{2}-2Rx},
MO_{2}^{2}+MO_{3}^{2}=O_{2}O_{3}^{2},
или
\left(\frac{R}{2}+\sqrt{R^{2}-2Rx}\right)^{2}+x^{2}=\left(\frac{R}{2}+x\right)^{2}.
Из этого уравнения находим, что x=\frac{4R}{9}
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1975 (отделение геофизики), вариант 3, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 155
