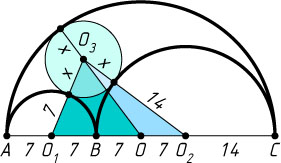
449. На отрезке AC
дана точка B
, причём AB=14
, BC=28
. На отрезках AB
, BC
, AC
как на диаметрах построены полуокружности в одной полуплоскости относительно прямой AB
. Найдите радиус окружности, касающейся всех трёх полуокружностей.
Ответ. 6.
Указание. Примените формулу Герона.
Решение. Пусть точки O_{1}
, O_{2}
и O
— центры данных полуокружностей с диаметрами AB
, BC
, AC
соответственно, x
— радиус искомой окружности, O_{3}
— её центр. Тогда
OO_{1}=14,~OO_{2}=7,~O_{1}O_{3}=7+x,~OO_{3}=21-x,~O_{2}O_{3}=14+x.
По формуле Герона
S_{\triangle OO_{1}O_{3}}=\sqrt{21\cdot7x(14-x)},~S_{\triangle OO_{2}O_{3}}=\sqrt{21\cdot14x(7-x)}.
Поскольку
\frac{S_{\triangle OO_{1}O_{3}}}{S_{\triangle OO_{2}O_{3}}}=\frac{OO_{1}}{OO_{2}}=2,
то \frac{\sqrt{14-x}}{\sqrt{2(7-x)}}=2
. Из этого уравнения находим, что x=6
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.391 с. 184
