450. На отрезке AC
взята точка B
и на отрезках AB
, BC
, CA
как на диаметрах построены полуокружности S_{1}
, S_{2}
, S_{3}
по одну сторону от AC
. Найдите радиус окружности, касающейся всех трёх полуокружностей, если известно, что её центр удалён от прямой AC
на расстояние a
.
Ответ. \frac{a}{2}
.
Указание. Примените формулу Герона или рассмотрите инверсию относительно окружности с центром A
радиуса AC
.
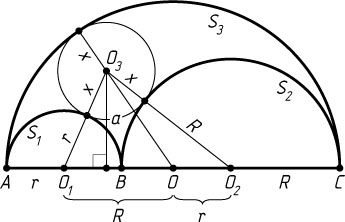
Решение. Первый способ. Пусть O_{1}
, O_{2}
, O
— центры данных полуокружностей S_{1}
, S_{2}
, S_{3}
соответственно (рис. 1), r
и R
— радиусы полуокружностей S_{1}
и S_{2}
, x
— радиус искомой окружности, O_{3}
— её центр. Тогда радиус полуокружности S_{3}
равен r+R
,
O_{1}O_{3}=r+x,~OO_{3}=r+R-x,~OO_{1}=R,
O_{2}O_{3}=R+x,~OO_{2}=r.
По формуле Герона
S_{\triangle OO_{1}O_{3}}=\sqrt{(r+R)(R-x)xr},~S_{\triangle OO_{2}O_{3}}=\sqrt{(r+R)(r-x)xR}.
Поскольку S_{\triangle OO_{1}O_{3}}=\frac{aR}{2}
и S_{\triangle OO_{2}O_{3}}=\frac{ar}{2}
, то
(r+R)(R-x)xr-(r+R)(r-x)xR=\frac{a^{2}R^{2}}{4}-\frac{a^{2}r^{2}}{4}.
Если r\ne R
, то из полученного уравнения находим, что x=\frac{a}{2}
.
Пусть теперь R=r
(рис. 2). Тогда точка B
совпадает с O
. В прямоугольном треугольнике O_{1}OO_{3}
известно, что OO_{1}=r
, O_{1}O_{3}=r+x
, OO_{3}=2r-x
. По теореме Пифагора (2r-x)^{2}+r^{2}=(r+x)^{2}
, откуда r=\frac{3x}{2}
, а так как OO_{3}=a=2r-x=3x-x=2x
, то x=\frac{a}{2}
.
Второй способ. Рассмотрим инверсию относительно окружности \omega
с центром A
радиуса AC
(рис. 3). При этой инверсии точка C
останется на месте, окружность S_{3}
, проходящая через центр инверсии, перейдёт в прямую S_{3}'
, проходящую через точку C
перпендикулярно AC
, окружность S_{1}
, проходящая через центр инверсии, — в прямую S_{1}'
, параллельную прямой S_{3}'
, окружность S_{2}
, не проходящая через центр инверсии, — в окружность S_{2}'
, касающуюся параллельных прямых S_{3}'
и S_{1}'
, а окружность S
, касающаяся окружностей S_{1}
, S_{2}
и S_{3}
, — в окружность S'
, касающуюся параллельных прямых S_{3}'
, S_{1}'
и окружности S_{2}'
. Радиус окружности S'
равен радиусу окружности S_{2}'
.
Пусть E
, Q
и P
— центры окружностей S
, S'
и S_{2}'
соответственно, M
— точка касания окружностей S'
и S_{2}'
, F
— проекция точки E
на прямую AC
(EF=a
), N
— точка пересечения отрезка EF
с окружностью S
.
Поскольку окружность S'
— образ окружности S
при рассматриваемой инверсии, окружности S'
и S
гомотетичны, причём центр гомотетии совпадает с центром A
инверсии. При этой гомотетии луч EF
переходит в параллельный ему луч QP
, луч AF
— в себя, точка F
— в точку P
, а радиус EN
окружности S
— в радиус QM
окружности S'
. Значит, \frac{EN}{EF}=\frac{QM}{QP}=\frac{1}{2}
. Следовательно, EN=\frac{1}{2}EF=\frac{a}{2}
.
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 5, с. 271
Источник: Журнал «Квант». — 1978, № 6, с. 42, М508
Источник: Задачник «Кванта». — М508
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1971
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 292, с. 33
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.47, с. 71
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 336(а), с. 51
