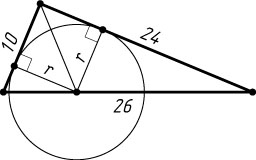
451. Дан треугольник со сторонами 10, 24 и 26. Две меньшие стороны являются касательными к окружности, центр которой лежит на большей стороне. Найдите радиус окружности.
Ответ. \frac{120}{17}
.
Указание. Площадь данного треугольника равна сумме площадей треугольников, на которые он разбивается отрезком, соединяющим вершину большего угла с центром данной окружности.
Решение. Заметим, что данный треугольник — прямоугольный (24^{2}+10^{2}=26^{2}
). Пусть r
— искомый радиус.
Отрезок, соединяющий вершину прямого угла с центром данной окружности, разбивает треугольник на два треугольника. Радиусы окружности, проведённые в точки касания, являются высотами этих треугольников. Сумма площадей получившихся треугольников равна площади данного треугольника, равной \frac{1}{2}\cdot10\cdot24=120
, т. е. 5r+12r=120
. Отсюда находим, что r=\frac{120}{17}
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.209, с. 172
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.21, с. 62
