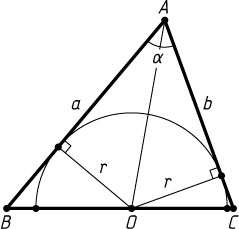
453. В треугольник со сторонами a
и b
и углом между ними \alpha
вписана полуокружность, диаметр которой лежит на третьей стороне. Найдите радиус полуокружности.
Ответ. \frac{ab\sin\alpha}{a+b}
.
Указание. Соедините вершину данного угла треугольника с центром полуокружности.
Решение. Соединив вершину данного угла с центром полуокружности, разобьём треугольник на два треугольника с основаниями a
и b
и высотами, равными r
— радиусу полуокружности. Сумма площадей полученных треугольников равна площади данного треугольника, т. е.
\frac{1}{2}ar+\frac{1}{2}br=\frac{1}{2}ab\sin\alpha.
Отсюда находим, что
r=\frac{ab\sin\alpha}{a+b}.