454. В круговой сектор с центральным углом 120^{\circ}
вписана окружность. Найдите её радиус, если радиус данной окружности равен R
.
Ответ. R\sqrt{3}(2-\sqrt{3})
.
Указание. Линия центров двух касающихся окружностей проходит через точку касания.
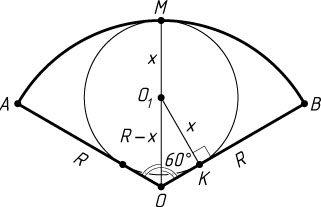
Решение. Пусть x
— радиус искомой окружности, O_{1}
— её центр, OA
и OB
— радиусы данного сектора, M
— точка касания окружностей, K
— точка касания искомой окружности с радиусом OB
. Тогда
OO_{1}=R-x,~KO_{1}=x,~\angle KOO_{1}=60^{\circ},
KO_{1}=OO_{1}\sin\angle KOO_{1},~\mbox{или}~x=\frac{(R-x)\sqrt{3}}{2}.
Отсюда находим, что
x=\frac{R\sqrt{3}}{2+\sqrt{3}}=R\sqrt{3}(2-\sqrt{3}).
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.070, с. 163
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.14, с. 68
