455. Окружность касается одного из катетов равнобедренного прямоугольного треугольника и проходит через вершину противолежащего острого угла. Найдите радиус окружности, если её центр лежит на гипотенузе треугольника, а катет треугольника равен a
.
Ответ. a(2-\sqrt{2})
.
Указание. Выразите через искомый радиус расстояние от центра окружности до вершин острых углов данного треугольника.
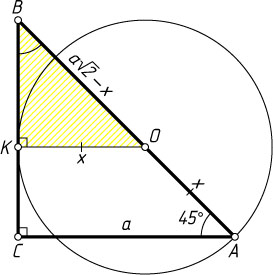
Решение. Пусть данная окружность имеет центр O
на гипотенузе AB
, касается катета BC
в точке K
и проходит через вершину A
. Обозначим через x
радиус этой окружности. Тогда в треугольнике OKB
известно, что
\angle B=45^{\circ},~OK=x,~OB=a\sqrt{2}-x.
Поэтому a\sqrt{2}-x=x\sqrt{2}
. Отсюда находим, что x=a(2-\sqrt{2})
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.052, с. 162
