456. На основании равнобедренного треугольника, равном 8, как на хорде построена окружность, касающаяся боковых сторон треугольника. Найдите радиус окружности, если высота, опущенная на основание треугольника, равна 3.
Ответ. \frac{20}{3}
.
Указание. Рассмотрите подобные треугольники.
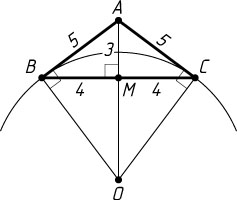
Решение. Пусть BC
— основание данного равнобедренного треугольника ABC
, O
— центр окружности. Тогда AO\perp BC
и BM=MC
, где M
— точка пересечения отрезков AO
и BC
.
В прямоугольном треугольнике AMC
известно, что AM=3
и MC=4
. Поэтому AC=5
.
Из подобия треугольников MCO
и MAC
следует, что \frac{OC}{AC}=\frac{MC}{AM}
. Следовательно,
OC=\frac{AC\cdot MC}{AM}=\frac{5\cdot4}{3}=\frac{20}{3}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.054, с. 162
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.14, с. 61
