459. В окружности радиуса R
проведён диаметр и на нём взята точка A
на расстоянии a
от центра. Найдите радиус второй окружности, которая касается диаметра в точке A
и изнутри касается данной окружности.
Ответ. \frac{R^{2}-a^{2}}{2R}
.
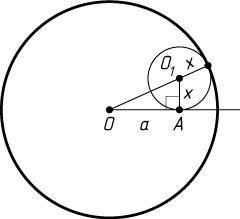
Решение. Пусть O
и O_{1}
— центры данных окружностей, x
— искомый радиус. В треугольнике OO_{1}A
известно, что
OA=a,~OO_{1}=R-x,~O_{1}A=x.
По теореме Пифагора
OO^{2}_{1}=OA^{2}+AO^{2}_{1},~\mbox{или}~(R-x)^{2}=x^{2}+a^{2}.
Отсюда находим, что x=\frac{R^{2}-a^{2}}{2R}
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 118, с. 200
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.9, с. 67
