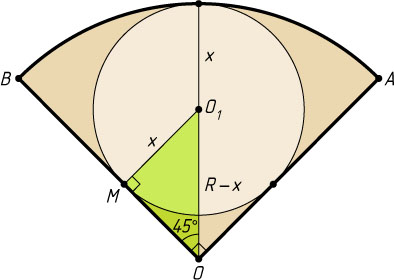
460. В сектор AOB
с радиусом R
и углом 90^{\circ}
вписана окружность, касающаяся отрезков OA
, OB
и дуги AB
. Найдите радиус окружности.
Ответ. R(\sqrt{2}-1)
.
Указание. Линия центров касающихся окружностей проходит через точку касания.
Решение. Пусть x
— радиус искомой окружности, O_{1}
— её центр, M
— точка касания меньшей окружности с радиусом OB
. В треугольнике OO_{1}M
известно, что
MO_{1}=x,~OO_{1}=R-x,~\angle OO_{1}M=45^{\circ}.
Поэтому R-x=x\sqrt{2}
. Следовательно,
x=\frac{R}{\sqrt{2}+1}=R(\sqrt{2}-1).
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.036, с. 159
