463. Расстояние между центрами окружностей радиусов r
и R
равно a
, причём a\gt r+R
. Найдите наименьшее из расстояний между точками, одна из которых лежит на первой окружности, а другая — на второй (расстояние между окружностями).
Ответ. a-r-R
.
Указание. С помощью обобщённого неравенства треугольника докажите, что расстояние между любыми двумя точками этих окружностей не меньше, чем a-r-R
.
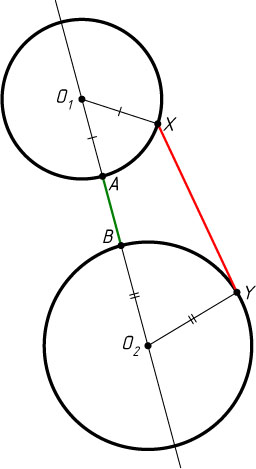
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно, а линия центров пересекает окружности соответственно в точках A
и B
, причём A
и B
лежат между O_{1}
и O_{2}
. Тогда, если X
и Y
— произвольные точки, лежащие соответственно на первой и второй окружности, то
XO_{1}+XY+YO_{2}\geqslant O_{1}O_{2}=AO_{1}+AB+BO_{2},
или
r+XY+R\geqslant r+AB+R.
Следовательно, XY\leqslant AB=a-r-R
, причём равенство достигается только в случае, когда X=A
и Y=B
.
