464. Наименьшее расстояние между точками двух концентрических окружностей равно 2, а наибольшее равно 16. Найдите радиусы окружностей.
Ответ. 7 и 9.
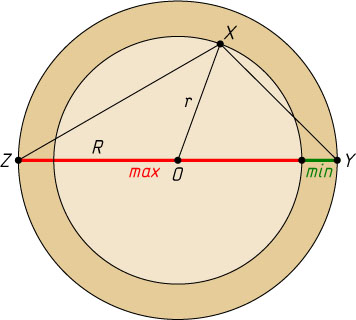
Указание. Наименьшее расстояние между точками двух концентрических окружностей равно разности их радиусов, а наибольшее — сумме.
Решение. Пусть O
— центр окружностей, r
и R
— их радиусы (r\lt R
). Если Y
и Z
— диаметрально противоположные точки большей окружности, а X
— произвольная точка меньшей, то
r+XY=OX+XY\geqslant OY,~\mbox{или}~XY\geqslant R-r,
XZ\leqslant OX+OZ=r+R.
Поэтому R+r=16
и R-r=2
. Из полученной системы уравнений находим, что R=9
, r=7
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 44, с. 33
