465. Наименьшее расстояние от данной точки до точек окружности равно a
, и наибольшее равно b
. Найдите радиус.
Ответ. \frac{b-a}{2}
или \frac{b+a}{2}
.
Указание. Рассмотрите два случая: данная точка вне и внутри круга.
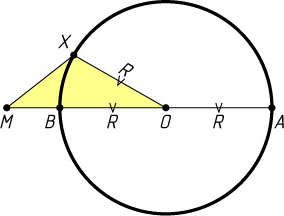
Решение. Пусть точка M
лежит вне окружности с центром O
(рис. 1) и AB=2R
— диаметр этой окружности, принадлежащий прямой OM
(B
между O
и M
). Если X
— произвольная точка окружности, то
MX\leqslant OX+OM=R+OM=AM.
Поэтому AM
— наибольшее расстояние от точки M
до точек окружности, а так как
MX+R=MX+OX\geqslant OM=OB+BM=R+BM,
то MX\geqslant BM
. Поэтому BM
— наименьшее расстояние от точки M
до точек окружности, Следовательно,
R=\frac{AM-BM}{2}=\frac{b-a}{2}.
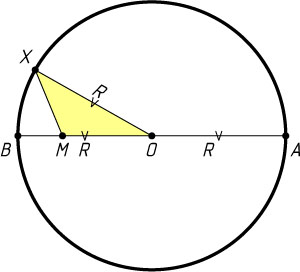
Если точка M
— внутри круга (рис. 2), то аналогично найдём, что
R=\frac{b+a}{2}.
Если же точка лежит на окружности, то a=0
и b=2R
, значит, R=\frac{b-a}{2}=\frac{b+a}{2}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 6, с. 29

