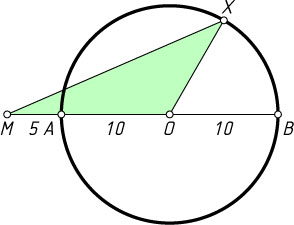
467. Радиус окружности равен 10, данная точка удалена от центра на расстояние, равное 15. Найдите её наименьшее и наибольшее расстояния от точек окружности.
Ответ. 5 и 25.
Указание. Для нахождения наименьшего и наибольшего расстояний от данной точки до точек окружности воспользуйтесь неравенством треугольника.
Решение. Пусть M
— данная точка, O
— центр окружности, AB
— её диаметр, принадлежащий прямой OM
(A
между O
и M
), X
— произвольная точка окружности. Тогда
MX+OX\geqslant OM=OA+AM.
Поэтому
MX\geqslant AM=15-10=5.
Аналогично находим, что MX\leqslant15+10=25
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 5(1) с. 28
