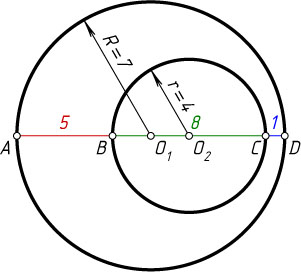
468. Даны два круга — один внутри другого. Через их центры проведён в большем круге диаметр, который окружностью меньшего круга делится на три части, равные 5, 8 и 1. Найдите расстояние между центрами кругов.
Ответ. 2.
Указание. Определите расположение центра большей окружности по отношению к меньшей окружности.
Решение. Пусть данный диаметр пересекает окружности последовательно в точках A
, B
, C
и D
так, что AB=5
, BC=8
, CD=1
; O_{1}
и O_{2}
— центры соответственно большей и меньшей окружностей, R
и r
— их радиусы. Тогда
R=\frac{AB+BC+CD}{2}=7,~r=\frac{1}{2}BC=4,
O_{1}O_{2}=O_{1}D-O_{2}D=R-(r+CD)=7-5=2.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 43 с. 33
