471. Даны две концентрические окружности радиусов 1 и 3 с общим центром O
. Третья окружность касается их обеих. Найдите угол между касательными к третьей окружности, проведёнными из точки O
.
Ответ. 60^{\circ}
.
Указание. Линия центров двух касающихся окружностей проходит через точку касания.
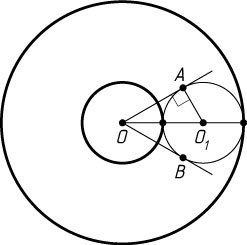
Решение. Пусть O_{1}
— центр третьей окружности, OA
и OB
— касательные к ней (A
и B
— точки касания). Тогда OO_{1}
— биссектриса угла AOB
,
AO_{1}=\frac{3-1}{2}=1,~OO_{1}=1+1=2,~\angle OAO_{1}=90^{\circ}.
Поэтому \angle AOO_{1}=30^{\circ}
, а \angle AOB=60^{\circ}
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 148, с. 203
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 105, с. 14
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.10, с. 67
