473. Найдите радиус окружности, которая высекает на обеих сторонах угла, равного \alpha
, хорды, равные a
, если известно, что расстояние между ближайшими концами этих хорд равно b
.
Ответ. \frac{\sqrt{a^{2}+b^{2}+2ab\sin\frac{\alpha}{2}}}{2\cos\frac{\alpha}{2}}
.
Указание. Выразите радиус окружности, описанной около треугольника, через сторону треугольника и синус противолежащего угла.
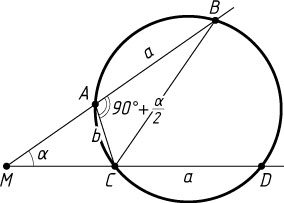
Решение. Пусть M
— вершина данного угла, AB
и CD
— данные хорды, AC=b
, AB=CD=a
, R
— радиус окружности.
Поскольку MA\cdot MB=MD\cdot MC
, то AM=CM
. Поэтому треугольник AMC
— равнобедренный. Следовательно,
\angle BAC=180^{\circ}-\angle MAC=90^{\circ}+\frac{\alpha}{2}.
По теореме косинусов
BC^{2}=AB^{2}+AC^{2}-2AB\cdot AC\cos\left(90^{\circ}+\frac{\alpha}{2}\right)=a^{2}+b^{2}+2ab\sin\frac{\alpha}{2},
R=\frac{BC}{2\sin\left(90^{\circ}+\frac{\alpha}{2}\right)}=\frac{\sqrt{a^{2}+b^{2}+2ab\sin\frac{\alpha}{2}}}{2\cos\frac{\alpha}{2}}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 108, с. 16
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 108, с. 14
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.18, с. 94
