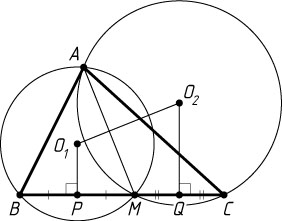
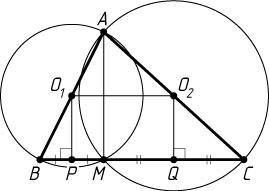
474. В треугольнике ABC
на наибольшей стороне BC
, равной b
, выбирается точка M
. Найдите наименьшее расстояние между центрами окружностей, описанных около треугольников BAM
и ACM
.
Ответ. \frac{b}{2}
.
Указание. Рассмотрите проекцию отрезка с концами в центрах окружностей на сторону BC
.
Решение. Проекции центров O_{1}
и O_{2}
данных окружностей на BC
— середины P
и Q
отрезков BM
и MC
соответственно. Тогда O_{1}O_{2}\geqslant PQ=\frac{b}{2}
.
Если AM
— высота треугольника BAC
, то
O_{1}O_{2}=PQ=\frac{b}{2}.
В остальных случаях O_{1}O_{2}\gt\frac{b}{2}
.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 111, с. 16
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 111, с. 14
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.6, с. 76

