475. В параллелограмме ABCD
известны стороны AB=a
, BC=b
и угол \angle ABC=\alpha
. Найдите расстояние между центрами окружностей, описанных около треугольников BCD
и DAB
.
Ответ. \sqrt{a^{2}+b^{2}+2ab\cos\alpha}|\ctg\alpha|
.
Указание. Диагональ BD
видна из центра каждой окружности под углом 2\alpha
или 360^{\circ}-2\alpha
.
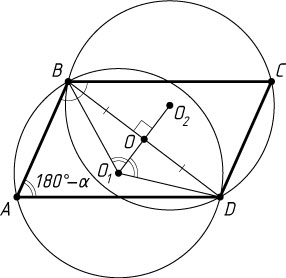
Решение. Пусть O_{1}
и O_{2}
— центры описанных окружностей треугольников DAB
и BCD
соответственно, O
— точка пересечения диагоналей параллелограмма. Поскольку треугольники DAB
и BCD
равны, то радиусы окружностей также равны. По свойству параллелограмма \angle BAD=180^{\circ}-\alpha
.
Пусть \alpha\gt90^{\circ}
. По теореме косинусов
BD=\sqrt{a^{2}+b^{2}-2ab\cos(180^{\circ}-\alpha)}=\sqrt{a^{2}+b^{2}+2ab\cos\alpha}.
Вписанный в окружность с центром O_{1}
угол BAD
равен половине центрального угла BO_{1}D
, значит,
\angle BO_{1}O_{2}=\frac{1}{2}\angle BO_{1}D=\angle BAD=180^{\circ}-\alpha.
Прямая O_{1}O_{2}
— серединный перпендикуляр к диагонали BD
, Поэтому
O_{1}O_{2}=2O_{1}O=2\cdot BO\ctg\angle BO_{1}O=
=2\cdot\frac{1}{2}BD\ctg\angle BO_{1}O=BD\ctg(180^{\circ}-\alpha)=-BD\ctg\alpha=
=-\sqrt{a^{2}+b^{2}+2ab\cos\alpha}\ctg\alpha.
Если же \alpha\geqslant90^{\circ}
, то аналогично получим, что
O_{1}O_{2}=\sqrt{a^{2}+b^{2}+2ab\cos\alpha}\ctg\alpha.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 112, с. 16
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 112, с. 15
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.12, с. 77
