477. Окружность радиуса r
вписана в угол, равный \alpha
. Другая окружность радиуса R
касается одной стороны угла в той же точке, что и первая, пересекая вторую сторону угла в точках A
и B
. Найдите AB
.
Ответ. 4\cos\frac{\alpha}{2}\sqrt{(R-r)\left(R\sin^{2}\frac{\alpha}{2}+r\cos^{2}\frac{\alpha}{2}\right)}
.
Указание. Найдите расстояние от центра большей окружности до хорды AB
.
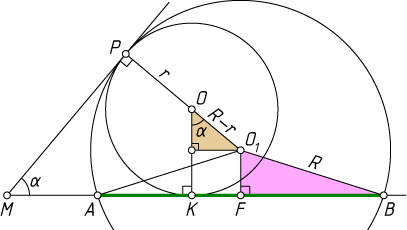
Решение. Пусть O
и O_{1}
— центры окружностей радиусов r
и R
, K
— точка касания первой окружности и прямой AB
, P
— общая точка касания, \angle AMP
— данный угол, F
— середина AB
. Тогда
AB=2\sqrt{O_{1}B^{2}-O_{1}F^{2}}=2\sqrt{R^{2}-(r-(R-r)\cos\alpha)^{2}}=
=4\cos\frac{\alpha}{2}\sqrt{(R-r)\left(R\sin^{2}\frac{\alpha}{2}+r\cos^{2}\frac{\alpha}{2}\right)}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 163, с. 204
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 120, с. 17
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 120, с. 15
