478. Дан равнобедренный треугольник ABC
с основанием AC
. Окружность радиуса R
с центром в точке O
проходит через точки A
и B
и пересекает прямую BC
в точке M
, отличной от B
и C
. Найдите расстояние от точки O
до центра окружности, описанной около треугольника ACM
.
Ответ. R
.
Указание. Докажите, что центр второй окружности лежит на первой.
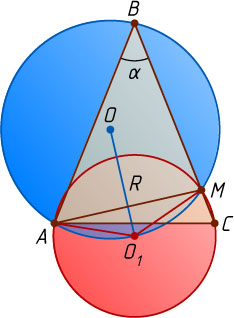
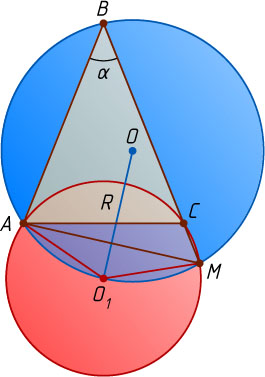
Решение. Пусть \angle ABC=\alpha
, O_{1}
— центр второй окружности. Тогда, так как угол BCA
— острый, то
\angle AO_{1}M=2\angle ACB=2\left(90^{\circ}-\frac{\alpha}{2}\right)=180^{\circ}-\alpha,
следовательно, точки A
, B
, M
и O_{1}
лежат на одной окружности. Поэтому точка O_{1}
принадлежит окружности, описанной около треугольника ABM
, т. е. OO_{1}=R
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 5, с. 170
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 6, задача 6
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6, с. 169

