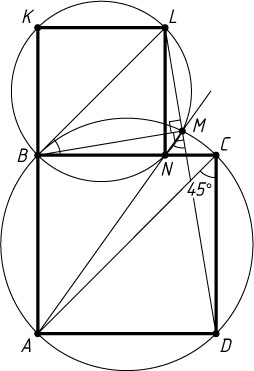
479. На плоскости расположены два квадрата ABCD
и BKLN
так, что точка K
лежит на продолжении AB
за точку B
, а N
лежит на луче BC
. Найдите угол между прямыми DL
и AN
.
Ответ. 45^{\circ}
.
Указание. Опишите окружности около данных квадратов и рассмотрите их точку пересечения, отличную от B
.
Решение. Первый способ. Пусть BN\lt BC
. Опишем окружности около данных квадратов и обозначим через M
их точку пересечения, отличную от B
. Тогда \angle BML=90^{\circ}
и \angle BMD=90^{\circ}
. Поэтому точки D
, M
и L
лежат на одной прямой.
Поскольку
\angle DMA=\angle DCA=45^{\circ},~\angle LMN=180^{\circ}-\angle NBL=135^{\circ},
то точки M
, N
и A
также лежат на одной прямой, а искомый угол равен 45^{\circ}
.
Второй способ. Пусть прямые DL
и AN
пересекаются в точке P
, а прямые KL
и CD
— в точке Q
. Обозначим AB=a
, BK=b
, \angle BAN=\alpha
, \angle CBN=\beta
. Тогда
\angle APD=180^{\circ}-(90^{\circ}-\alpha)-(90^{\circ}-\beta)=\alpha+\beta.
Из прямоугольных треугольников ABN
и DQL
находим, что
\tg\alpha=\frac{BN}{AB}=\frac{b}{a},~\tg\beta=\frac{LQ}{DQ}=\frac{CN}{DQ}=\frac{a-b}{a+b}.
Тогда
\tg\angle APD=\tg(\alpha+\beta)=\frac{\tg\alpha+\tg\beta}{1-\tg\alpha\tg\beta}=\frac{\frac{b}{a}+\frac{a-b}{a+b}}{1-\frac{b}{a}\cdot\frac{a-b}{a+b}}=1.
Следовательно, \angle APD=45^{\circ}
.
Третий способ. Обозначим AB=a
, BK=b
. На луче AB
отложим отрезок AK_{1}=b
. Тогда
KK_{1}=AK-AK_{1}=(a+b)-b=a.
Прямоугольные треугольники ADK_{1}
и KK_{1}L
равны по двум катетам, поэтому
DK_{1}=K_{1}L,~\angle AK_{1}D=\angle KLK_{1}=90^{\circ}-\angle KK_{1}L.
Тогда
\angle DK_{1}L=180^{\circ}-\angle AK_{1}D-\angle KK_{1}L=180^{\circ}-90^{\circ}=90^{\circ}.
Значит, треугольник DK_{1}L
прямоугольный и равнобедренный, поэтому \angle DLK_{1}=45^{\circ}
, а так как LK_{1}\parallel AN
, то угол между прямыми DL
и AN
также равен 45^{\circ}
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 17, с. 179
