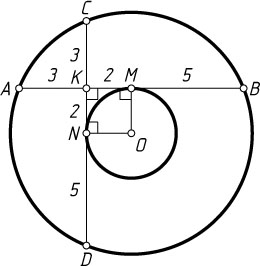
481. Даны две концентрические окружности. В большей окружности даны две взаимно перпендикулярные хорды, касательные к меньшей. Каждая из хорд делится другой на части, равные 3 и 7. Найдите радиус меньшей окружности.
Ответ. 2.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
Решение. Пусть M
и N
— точки касания хорд AB
и CD
с меньшей окружностью, K
— точка пересечения хорд, O
— центр окружностей, AK=CK=3
, BK=DK=7
. Тогда M
и N
— середины данных хорд. Следовательно,
AM=5,~ON=KM=AM-AK=5-3=2.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 45, с. 33
