483. Даны две концентрические окружности и пересекающая их прямая. Докажите, что отрезки этой прямой, заключённые между между окружностями, равны.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
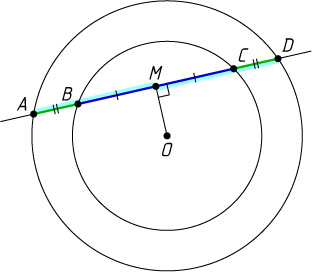
Решение. Пусть прямая пересекает окружности последовательно в точках A
, B
, C
и D
. Пусть M
— основание перпендикуляра, опущенного из центра окружностей на секущую. Тогда M
— общая середина хорд AD
и BC
.
Следовательно, AB=CD
.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 3, с. 30
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 47, с. 33
