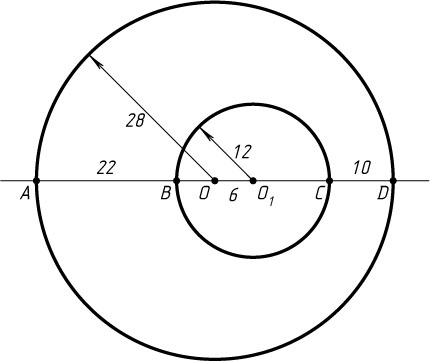
484. Одна окружность находится внутри другой. Их радиусы равны 28 и 12, а кратчайшее расстояние между точками этих окружностей равно 10. Найдите расстояние между центрами.
Ответ. 6.
Указание. Определите расположение центра большей окружности по отношению к меньшей окружности.
Решение. Известно, что кратчайшее расстояние между точками двух таких окружностей равно наименьшему из двух отрезков линии центров, заключённых между окружностями. Пусть O
и O_{1}
— центры соответственно большей и меньшей окружностей. Проведём диаметр большей окружности так, чтобы он прошёл через центр меньшей. Точки его пересечения с окружностями обозначим последовательно A
, B
, C
и D
. Если DC=10
, то
AB=56-24-10=22,~AO_{1}=12+22=34,~OA=28
следовательно,
OO_{1}=34-28=6.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 48, с. 33
