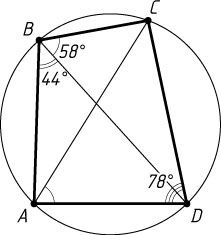
486. В выпуклом четырёхугольнике ABCD
известно, что \angle CBD=58^{\circ}
, \angle ABD=44^{\circ}
, \angle ADC=78^{\circ}
. Найдите угол CAD
.
Ответ. 58^{\circ}
.
Указание. Четырёхугольник ABCD
— вписанный.
Решение. Поскольку
\angle ABC=\angle ABD+\angle DBC=44^{\circ}+58^{\circ}=102^{\circ},
то
\angle ABC+\angle ADC=102^{\circ}+78^{\circ}=180^{\circ}.
Следовательно, четырёхугольник ABCD
— вписанный. Поэтому
\angle CAD=\angle DBC=58^{\circ}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 47, с. 196
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 1, задача 3
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3, с. 164
