487. Угол с вершиной A
равен \alpha
. Расстояние между основаниями перпендикуляров, опущенных из некоторой точки B
на стороны угла, равно a
. Найдите AB
.
Ответ. \frac{a}{\sin\alpha}
.
Указание. Точки A
, B
и основания указанных перпендикуляров лежат на одной окружности.
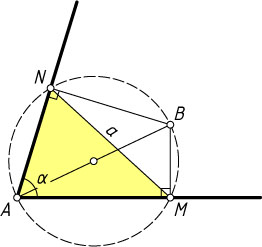
Решение. Отрезок AB
виден из оснований M
и N
указанных перпендикуляров под углом 90^{\circ}
, поэтому точки A
, B
, M
и N
лежат на окружности с диаметром AB
, а отрезок MN
виден из точки A
под углом \alpha
. Следовательно,
AB=\frac{MN}{\sin\alpha}=\frac{a}{\sin\alpha}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 52, с. 196
