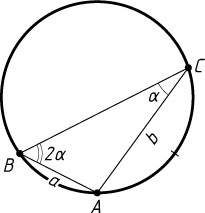
489. В окружности проведены две хорды AB=a
и AC=b
. Длина дуги AC
, не содержащей точки B
, вдвое больше длины дуги AB
, не содержащей точки C
. Найдите радиус окружности.
Ответ. \frac{a^{2}}{\sqrt{4a^{2}-b^{2}}}
.
Указание. С помощью теоремы синусов составьте тригонометрическое уравнение.
Решение. Вписанный угол равен половине дуги, на которую он опирается, поэтому угол B
треугольника ABC
вдвое больше угла C
. Пусть \angle ACB=\alpha
. Тогда \angle ABC=2\alpha
. По теореме синусов
\frac{a}{\sin\alpha}=\frac{b}{\sin2\alpha}.
Поэтому \cos\alpha=\frac{b}{2a}
. Тогда
\sin\alpha=\sqrt{1-\left(\frac{b}{2a}\right)^{2}}=\frac{\sqrt{4a^{2}-b^{2}}}{2a}.
Если R
— радиус окружности, то
R=\frac{a}{2\sin\alpha}=\frac{a^{2}}{\sqrt{4a^{2}-b^{2}}}.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.044, с. 161
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.18, с. 87
