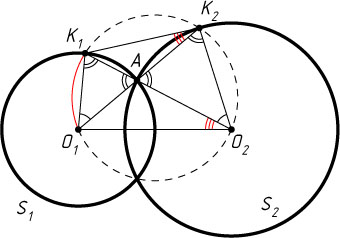
490. Две окружности S_{1}
и S_{2}
с центрами O_{1}
и O_{2}
пересекаются в точке A
. Прямая O_{1}A
пересекает окружность S_{2}
в точке K_{2}
, а прямая O_{2}A
пересекает окружность S_{1}
в точке K_{1}
. Докажите, что \angle O_{1}O_{2}A=\angle K_{1}K_{2}A
.
Указание. Докажите, что \angle AO_{1}K_{1}=\angle AO_{2}K_{2}
.
Решение. В равнобедренных треугольниках O_{1}K_{1}A
и O_{2}K_{2}A
углы при основаниях AK_{1}
и AK_{2}
равны. Поэтому \angle AO_{1}K_{1}=\angle AO_{2}K_{2}
. Следовательно, точки O_{1}
, O_{2}
, K_{1}
и K_{2}
лежат на одной окружности. Поэтому \angle O_{1}O_{2}A=\angle K_{1}K_{2}A
.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 64, с. 18
