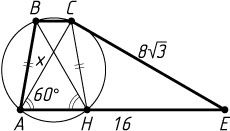
491. В трапеции ABCE
основание AE
равно 16
, CE=8\sqrt{3}
. Окружность, проходящая через точки A
, B
и C
, вторично пересекает прямую AE
в точке H
; \angle AHB=60^{\circ}
. Найдите AC
.
Ответ. 8.
Указание. Примените теорему косинусов.
Решение. Трапеция ABCH
вписана в окружность, поэтому она — равнобедренная. Следовательно, \angle CAH=\angle AHB=60^{\circ}
. Обозначим AC=x
и применим теорему косинусов к треугольнику ACE
:
(8\sqrt{3})^{2}=x^{2}+16^{2}-16x.
Отсюда находим, что x=8
.
Источник: Вступительный экзамен на факультет вычислительной математики и кибернетики (ВМК) МГУ. — 1984, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 21
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 503
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 4.45, с. 41
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4.45.1, с. 40
