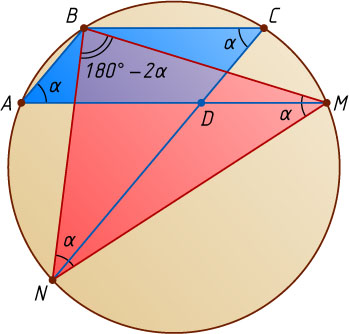
493. В параллелограмме ABCD
острый угол равен \alpha
. Окружность радиуса r
проходит через вершины A
, B
, C
и пересекает прямые AD
и CD
в точках M
и N
. Найдите площадь треугольника BMN
.
Ответ. 2r^{2}\sin^{2}\alpha\sin2\alpha
.
Указание. Треугольник BMN
— равнобедренный.
Решение. Предположим, что точка M
лежит на прямой AD
, а точка N
— на прямой CD
.
Пусть \angle BAD=\alpha
. Тогда
\angle BNM=\angle BAD=\alpha,~\angle BMN=\angle BCN=\alpha.
Отсюда находим, что
BN=BM=2r\sin\alpha,~\angle MBN=180^{\circ}-2\alpha.
Поэтому
S_{\triangle BMN}=\frac{1}{2}\cdot BN\cdot BM\sin\angle NBM=\frac{1}{2}(2r\sin\alpha)^{2}\sin(180^{\circ}-2\alpha)=
=2r^{2}\sin^{2}\alpha\sin2\alpha.
Если же точка M
лежит на прямой CD
, а точка N
— на прямой AD
, то получим тот же результат.
