494. Окружность, проходящая через вершины A
, B
и C
параллелограмма ABCD
, пересекает прямые AD
и CD
в точках M
и N
соответственно. Точка M
удалена от вершин B
, C
и D
на расстояния 4, 3 и 2 соответственно. Найдите MN
.
Ответ. \frac{8}{3}
.
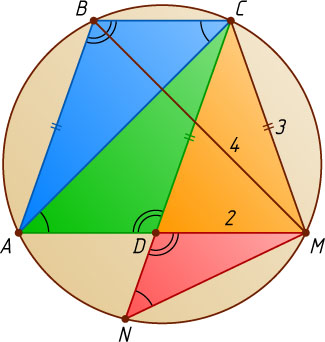
Указание. Треугольники NDM
и CBA
подобны.
Решение. Поскольку
\angle ABC=\angle ADC=\angle NDM,~\angle ACB=\angle MAC=\angle MNC,
треугольники NDM
и CBA
подобны. Следовательно, \frac{MN}{AC}=\frac{MD}{AB}
. Кроме того, поскольку ABCM
— равнобедренная трапеция,
AB=MC=3,~AC=MB=4.
Поэтому
MN=\frac{AC\cdot MD}{AB}=\frac{4\cdot2}{3}=\frac{8}{3}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 237, с. 210
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 154, с. 19
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.27, с. 105
