495. В равнобедренном треугольнике ABC
известно, что \angle B=120^{\circ}
. Найдите общую хорду окружности, описанной около треугольника ABC
, и окружности, проходящей через центр вписанной окружности и основания биссектрис углов A
и C
, если AC=1
.
Ответ. \sqrt[{4}]{{12}}(2-\sqrt{3})
.
Указание. Найдите стороны треугольника с вершинами в центрах окружностей и в одном из концов искомой хорды.
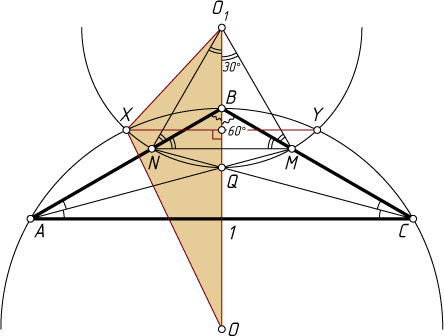
Решение. Пусть O
и O_{1}
— центры первой и второй окружностей, R
и r
— их радиусы, AM
и CN
— биссектрисы углов при основании, Q
— точка их пересечения, XY
— искомая общая хорда. Тогда
R=\frac{1}{\sqrt{3}},~\angle NO_{1}M=60^{\circ},~r=MN=\frac{AC\cdot BM}{BC}=\frac{\sqrt{3}-1}{2},
\angle O_{1}MB=\angle O_{1}MN-\angle BMN=60^{\circ}-30^{\circ}=30^{\circ},~\angle MO_{1}B=30^{\circ}.
Поэтому
O_{1}B=BM=\frac{2}{3}\cdot\frac{r\sqrt{3}}{2}=\frac{r\sqrt{3}}{3}=\frac{\sqrt{3}}{6}(\sqrt{3}-1).
Искомая хорда равна удвоенной высоте треугольника XOO_{1}
, проведённой из вершины X
, причём все стороны этого треугольника известны:
O_{1}X=\frac{\sqrt{3}-1}{2},~O_{1}O=OB+BO_{1}=\frac{\sqrt{3}}{6}(\sqrt{3}+1),~OX=\frac{\sqrt{3}}{3}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 239, с. 210
