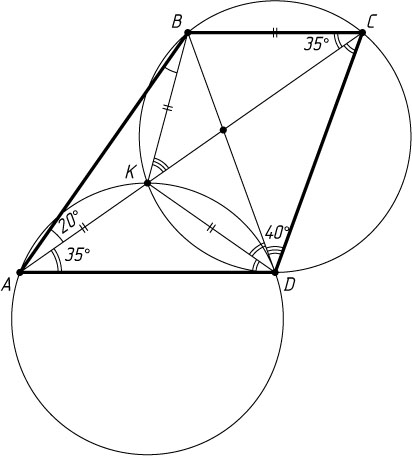
499. В выпуклом четырёхугольнике ABCD
известны углы: \angle BAC=20^{\circ}
, \angle BCA=35^{\circ}
, \angle BDC=40^{\circ}
, \angle BDA=70^{\circ}
. Найдите угол между диагоналями этого четырёхугольника.
Ответ. 75^{\circ}
.
Указание. Проведите биссектрису угла ADB
(или опишите окружность около треугольника ABC
).
Решение. Первый способ. Пусть K
— точка пересечения биссектрисы угла ADB
с диагональю AC
. Поскольку \angle KDB=\angle KCB=35^{\circ}
, то точки K
, B
, C
, D
лежат на одной окружности. Поэтому
\angle BKC=\angle BDC=40^{\circ},~\angle ABK=\angle BKC-\angle BAC=40^{\circ}-20^{\circ}=20^{\circ}.
Тогда AK=BK
и радиус окружности, описанной около треугольника AKD
, равен радиусу первой окружности (\angle ADK=\angle KDB=35^{\circ}
). Поэтому DA=DC
и
\angle CAD=\angle ACD=\frac{180^{\circ}-110^{\circ}}{2}=35^{\circ}.
Следовательно, угол между диагоналями равен
\angle BDC+\angle ACD=40^{\circ}+35^{\circ}=75^{\circ}.
Второй способ. Опишем окружность около треугольника ABC
. Пусть луч BD
пересекает эту окружность в точке E
. Поскольку
\angle AEC=180^{\circ}-\angle ABC=\angle BAC+\angle BCA=20^{\circ}+35^{\circ}=55^{\circ}\lt110^{\circ}=\angle ADC,
точка D
лежит на отрезке BE
.
По теореме о внешнем угле треугольника
\angle DCE=\angle BDC-\angle BEC=40^{\circ}-20^{\circ}=20^{\circ}=\angle DEC,
значит, DC=DE
. Аналогично получим, что DE=DA
. Следовательно, D
— центр описанной окружности треугольника AEC
.
Пусть M
— точка пересечения диагоналей четырёхугольника ABCD
. Из равнобедренного треугольника ADC
находим, что \angle ACD=35^{\circ}
. Тогда по теореме о внешнем угле треугольника
\angle BMC=\angle BEC+\angle CEM=\angle BAC+(\angle ACD+\angle DCE)=
=20^{\circ}+(35^{\circ}+20^{\circ})=75^{\circ}.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 93, с. 26
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 778, с. 97
