500. На стороне AB
треугольника ABC
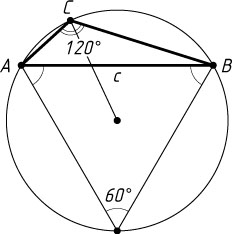
во внешнюю сторону построен равносторонний треугольник. Найдите расстояние между его центром и вершиной C
, если AB=c
и \angle C=120^{\circ}
.
Ответ. \frac{c\sqrt{3}}{3}
.
Указание. Опишите окружность около равностороннего треугольника.
Решение. Точка C
лежит на окружности, описанной около построенного равностороннего треугольника (60^{\circ}+120^{\circ}=180^{\circ}
), поэтому искомое расстояние равно радиусу этой окружности, т. е.
R=\frac{c}{2\sin60^{\circ}}=\frac{c}{\sqrt{3}}=\frac{c\sqrt{3}}{3}.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 22, с. 19
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.23, с. 105
