501. В треугольнике ABC
на стороне BC
взята точка M
, причём BM=2MC
и \angle AMB=60^{\circ}
. Зная, что \angle BAC=60^{\circ}
, найдите углы B
и C
треугольника ABC
.
Ответ. 75^{\circ}
; 45^{\circ}
.
Указание. Основание перпендикуляра, опущенного из точки B
на AM
, — центр окружности, описанной около треугольника ABC
.
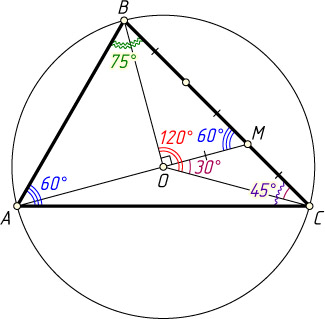
Решение. Пусть точка O
— основание перпендикуляра, опущенного из точки B
на AM
. Тогда
OM=\frac{1}{2}BM=MC,~\angle MOC=\angle OCM=30^{\circ},~\angle BOC=120^{\circ}.
Следовательно, точка O
— центр окружности, описанной около треугольника ABC
. Поэтому
\angle ACB=\frac{1}{2}\angle AOB=45^{\circ}.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 68, с. 19
