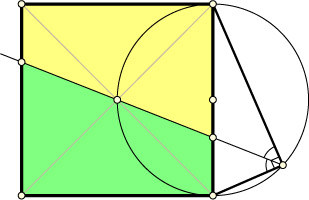
504. На стороне квадрата во внешнюю сторону построен прямоугольный треугольник, гипотенуза которого совпадает со стороной квадрата. Докажите, что биссектриса прямого угла этого треугольника делит площадь квадрата пополам.
Указание. Прямая, проходящая через центр параллелограмма, делит его площадь пополам.
Решение. Окружность, описанная около построенного треугольника, проходит через центр квадрата. Поскольку дуга окружности, заключённая внутри квадрата, делится его центром пополам, то биссектриса прямого угла построенного треугольника проходит через центр квадрата, и поэтому делит его площадь пополам.

Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 30, с. 11
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 95, с. 95