506. В окружность вписан треугольник. Вторая окружность, концентрическая первой, касается одной стороны треугольника и делит каждую из двух других сторон на три равные части. Найдите отношение радиусов этих окружностей.
Ответ. \frac{5}{9}
.
Указание. Примените теорему о касательной и секущей.
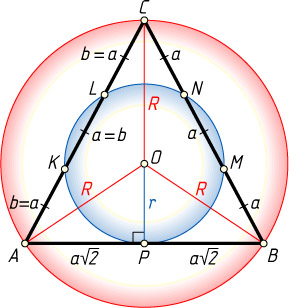
Решение. Пусть меньшая окружность касается стороны AB
треугольника ABC
в точке P
, пересекает сторону BC
в точках M
и N
, а сторону AC
— в точках K
и L
, и BM=MN=NC=a
, AK=KL=LC=b
.
Поскольку CM\cdot CN=CK\cdot CL
, то a=b
, а так как PB^{2}=BN\cdot BM
, то PB=AP=a\sqrt{2}
.
Если R
— радиус большей окружности, то
R=\frac{3a}{2\sin\angle BAC}=\frac{9a}{2\sqrt{7}}.
Если r
— радиус меньшей окружности, то
r=\sqrt{R^{2}-2a^{2}}=\frac{5a}{2\sqrt{7}}.
Следовательно, \frac{r}{R}=\frac{5}{9}
.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 222, с. 209
