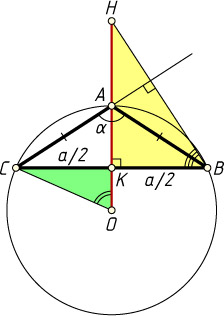
507. В равнобедренном треугольнике ABC
известно, что \angle A=\alpha\gt90^{\circ}
и BC=a
. Найдите расстояние между точкой пересечения высот и центром описанной окружности.
Ответ. \frac{1}{2}a\left(\tg\frac{\alpha}{2}-\ctg\alpha\right)
.
Указание. Высота, проведённая к боковой стороне треугольника, образует с основанием угол, равный \frac{\alpha}{2}
.
Решение. Пусть H
— точка пересечения высот, O
— центр описанной окружности, K
— середина BC
. Точки H
и O
лежат по разные стороны от прямой BC
.
OH=HK+OK=BK\tg\angle HBC+KC\ctg\angle AOC=
=\frac{a}{2}\tg\frac{\alpha}{2}+\frac{a}{2}\ctg(180^{\circ}-\alpha)=\frac{a}{2}\left(\tg\frac{\alpha}{2}-\ctg\alpha\right).
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 73, с. 13
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 73, с. 11
