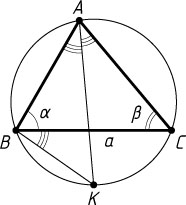
508. Около треугольника ABC
, в котором BC=a
, \angle B=\alpha
, \angle C=\beta
, описана окружность. Биссектриса угла A
пересекает эту окружность в точке K
. Найдите AK
.
Ответ. \frac{a\cos\frac{\beta-\alpha}{2}}{\sin(\beta+\alpha)}
.
Указание. Сторона треугольника равна диаметру описанной окружности, умноженному на синус противолежащего угла.
Решение. Пусть R
— радиус окружности, описанной около треугольника ABC
. Тогда
\angle BAC=180^{\circ}-(\beta+\alpha),~2R=\frac{BC}{\sin(\beta+\alpha)}=\frac{a}{\sin(\beta+\alpha)},
\angle ABK=\angle ABC+\angle CBK=\alpha+\frac{1}{2}(180^{\circ}-(\alpha+\beta))=90^{\circ}+\frac{\alpha-\beta}{2}.
Следовательно,
AK=2R\sin\angle ABK=2R\sin\left(90^{\circ}+\frac{\alpha-\beta}{2}\right)=
=2R\cos\frac{\beta-\alpha}{2}=\frac{a\cos\frac{\beta-\alpha}{2}}{\sin(\beta+\alpha)}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 74, с. 13
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 74, с. 11
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.14, с. 104
