510. Найдите сумму квадратов расстояний от точки M
, взятой на диаметре некоторой окружности, до концов любой из параллельных этому диаметру хорд, если радиус окружности равен R
, а расстояние от точки M
до центра окружности равно a
.
Ответ. 2(a^{2}+R^{2})
.
Указание. Примените теорему косинусов.
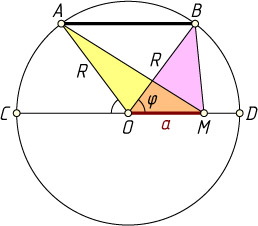
Решение. Пусть O
— центр окружности. AB
— произвольная хорда, параллельная данному диаметру. Обозначим \angle BOM=\varphi
. Тогда \angle AOM=180^{\circ}-\varphi
. По теореме косинусов из треугольников BOM
и AOM
находим, что
BM^{2}=a^{2}+R^{2}-2aR\cos\varphi,
AM^{2}=a^{2}+R^{2}-2aR\cos(180^{\circ}-\varphi)=a^{2}+R^{2}+2aR\cos\varphi.
Сложив почленно эти равенства, получим, что
BM^{2}+AM^{2}=2(a^{2}+R^{2}).
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 126, с. 201
