511. Найдите косинус угла при основании равнобедренного треугольника, если точка пересечения его высот лежит на вписанной в треугольник окружности.
Ответ. \frac{2}{3}
.
Указание. Если угол при основании равнобедренного треугольника равен \alpha
, то высота, проведённая к боковой стороне, образует с основанием угол 90^{\circ}-\alpha
.
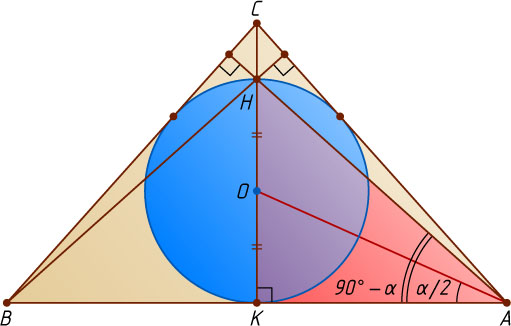
Решение. Пусть O
— центр окружности, вписанной в треугольник ABC
(AC=BC
), H
— точка пересечения высот, \angle CAB=\angle CBA=\alpha
, K
— середина AB
. Тогда
OK=AK\tg\frac{\alpha}{2},~HK=AK\tg(90^{\circ}-\alpha)=AK\ctg\alpha.
Поскольку HK=2OK
, то 2\tg\frac{\alpha}{2}=\ctg\alpha
.
Пусть \tg\frac{\alpha}{2}=t
. Тогда полученное уравнение имеет вид:
2t=\frac{1-t^{2}}{2t}.
Отсюда находим, что t^{2}=\frac{1}{5}
. Следовательно,
\cos\alpha=\frac{1-t^{2}}{1+t^{2}}=\frac{2}{3}.
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 10, с. 169
Источник: Вступительный экзамен на физический факультет МГУ. — 1967, вариант 4, № 4
Источник: Моденов П. С. Экзаменационные задачи по математике с анализом их решения. — М.: Просвещение, 1969. — вариант 4, № 4, с. 66
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 70, с. 15
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. —
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 89, с. 12
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 5, задача 4
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4, с. 168
