512. На одной стороне прямого угла с вершиной в точке O
взяты две точки A
и B
, причём OA=a
, OB=b
. Найдите радиус окружности, проходящей через точки A
и B
и касающейся другой стороны угла.
Ответ. \frac{a+b}{2}
.
Указание. Опустите перпендикуляр из центра окружности на хорду AB
.
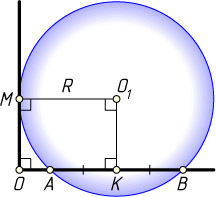
Решение. Предположим, что b\gt a
. Пусть M
— точка касания, R
— искомый радиус, K
— проекция центра O_{1}
данной окружности на AB
. Тогда
AK=KB=\frac{b-a}{2},~R=MO_{1}=OK=OA+AK=
=a+\frac{b-a}{2}=\frac{b+a}{2}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 21, с. 9
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 21, с. 7
