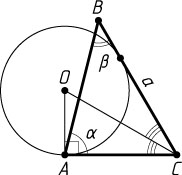
513. В треугольнике ABC
известно, что BC=a
, \angle A=\alpha
, \angle B=\beta
. Найдите радиус окружности, касающейся стороны AC
в точке A
и касающейся стороны BC
.
Ответ. \frac{a\sin\beta\ctg\frac{\alpha+\beta}{2}}{\sin\alpha}
.
Указание. Примените теорему синусов.
Решение. Пусть O
— центр окружности. Тогда OA
— её радиус,
OA=AC\tg\angle ACO=AC\tg\frac{1}{2}\angle ACB.
Из данного треугольника по теореме синусов находим, что AC=\frac{a\sin\beta}{\sin\alpha}
.
Поскольку \angle ACB=180^{\circ}-\alpha-\beta
, то
OA=\frac{a\sin\beta\tg\left(90^{\circ}-\frac{\alpha+\beta}{2}\right)}{\sin\alpha}=\frac{a\sin\beta\ctg\frac{\alpha+\beta}{2}}{\sin\alpha}.
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 145, с. 203
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.20, с. 61
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 102, с. 13
