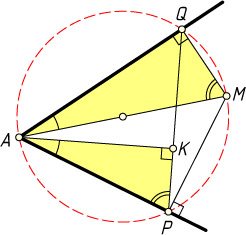
515. Из произвольной точки M
внутри острого угла с вершиной A
опущены перпендикуляры MP
и MQ
на его стороны. Из вершины A
проведён перпендикуляр AK
на PQ
. Докажите, что \angle PAK=\angle MAQ
.
Указание. Точки M
, P
, A
и Q
лежат на одной окружности.
Решение. Точки M
, P
, A
и Q
лежат на одной окружности. Поэтому \angle APQ=\angle AMQ
. Поскольку
\angle PAK=90^{\circ}-\angle APQ,~\angle MAQ=90^{\circ}-\angle AMQ,
то \angle PAK=\angle MAQ
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.3, с. 31
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.3, с. 31
