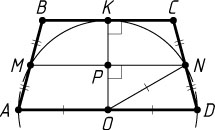
516. Окружность, построенная на основании AD
трапеции ABCD
как на диаметре, проходит через середины боковых сторон AB
и CD
трапеции и касается основания BC
. Найдите углы трапеции.
Ответ. 75^{\circ}
, 75^{\circ}
, 105^{\circ}
, 105^{\circ}
.
Указание. Радиус окружности, проведённый в середину боковой стороны, образует угол в 30^{\circ}
с основанием трапеции.
Решение. Пусть M
и N
— середины боковых сторон соответственно AB
и CD
трапеции ABCD
. Тогда MN\parallel AD
.
Пусть O
— центр окружности, K
— точка касания с основанием BC
, P
— точка пересечения радиуса OK
со средней линией MN
. Тогда
OP=\frac{1}{2}OK=\frac{1}{2}ON.
Из прямоугольного треугольника PNO
находим, что \angle PNO=30^{\circ}
. Тогда
\angle NOD=\angle PNO=30^{\circ},~\angle CDA=\frac{180^{\circ}-30^{\circ}}{2}=75^{\circ}.
Аналогично находим, что \angle BAD=75^{\circ}
.
Источник: Вступительный экзамен в МФТИ. — 1979, билет 5, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 79-5-3, с. 214
Источник: Пособие по математике для поступающих в вузы / Под ред. Г. Н. Яковлева. — 3-е изд. — М.: Наука, 1988. — № 35, с. 406
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.33, с. 32
