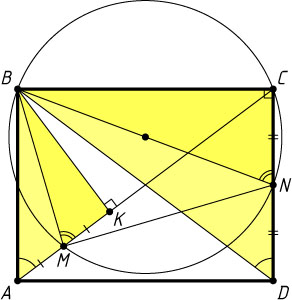
517. В прямоугольнике ABCD
опущен перпендикуляр BK
на диагональ AC
. Точки M
и N
— середины отрезков AK
и CD
соответственно. Докажите, что угол BMN
— прямой.
Указание. Точки M
, B
, C
и N
принадлежат одной окружности.
Решение. Первый способ. Поскольку \angle BAK=\angle BDC
, то треугольники BAK
и BDC
подобны. BM
и BN
— медианы этих треугольников, проведённые из вершин соответствующих углов. Поэтому треугольники BMK
и BNC
подобны. Тогда \angle BMC=\angle BNC
. Следовательно, точки M
, B
, C
и N
принадлежат одной окружности и BN
— её диаметр. Поэтому \angle BMN=90^{\circ}
.
Второй способ. Поскольку
\overrightarrow{MN}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{KC})=\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{KC})~\mbox{и}~\overrightarrow{BM}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BK})
то
\overrightarrow{MN}\cdot\overrightarrow{BM}=\frac{1}{4}(\overrightarrow{BC}+\overrightarrow{KC})(\overrightarrow{BA}+\overrightarrow{BK})=
=\frac{1}{4}(\overrightarrow{BC}\cdot\overrightarrow{BK}+\overrightarrow{KC}\cdot\overrightarrow{BA})=\frac{1}{4}(\overrightarrow{BC}\cdot\overrightarrow{BK}-\overrightarrow{KC}\cdot\overrightarrow{AB}),
так как
\overrightarrow{BC}\cdot\overrightarrow{BA}=\overrightarrow{KC}\cdot\overrightarrow{BK}=0.
Обозначим \angle BAC=\angle KBC=\alpha
. Тогда
\overrightarrow{BC}\cdot\overrightarrow{BK}-\overrightarrow{KC}\cdot\overrightarrow{AB}=BC\cdot BK\cos\alpha-KC\cdot AB\cos\alpha=
=(BC\cdot BK-KC\cdot AB)\cos\alpha=(BC\cdot KC\ctg\alpha-KC\cdot BC\ctg\alpha)\cos\alpha=0.
Следовательно, BM\perp MN
.
Примечание. См. статью Д.Швецова «Подобие с медианами», Квант, 2021, N7, с.42-47.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 26, с. 10
Источник: Всесибирская физико-математическая олимпиада. — 2010-2011, первый этап, задача 3, 10 класс
Источник: Журнал «Квант». — 2021, № 7, с. 43, задача 2
