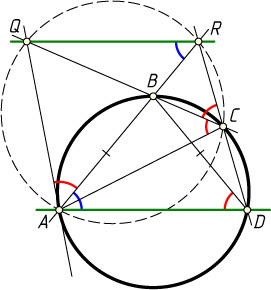
518. На окружности взяты последовательно точки A
, B
, C
и D
, причём AB=BD
. Касательная к окружности в точке A
пересекается с прямой BC
в точке Q
; R
— точка пересечения прямых AB
и CD
. Докажите, что прямые QR
и AD
параллельны.
Указание. Докажите, что точки A
, C
, R
и Q
лежат на одной окружности.
Решение. Пусть точка C
лежит на дуге BD
, не содержащей точку A
. Поскольку
\angle QAB=\angle BDA=\angle BAD=\angle BCR,
то точки A
, C
, R
и Q
принадлежат одной окружности. Поэтому
\angle QRA=\angle QCA=\angle BDA=\angle BAD.
Следовательно, QR\parallel AD
.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 49, с. 15
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 823, с. 101
