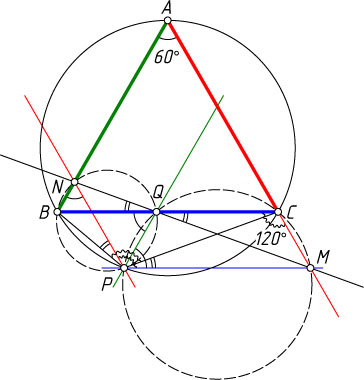
519. Из некоторой точки окружности, описанной около равностороннего треугольника ABC
, проведены прямые, параллельные BC
, CA
и AB
и пересекающие прямые CA
, AB
и BC
в точках M
, N
и Q
соответственно. Докажите, что точки M
, N
и Q
лежат на одной прямой.
Указание. Если P
— точка на данной окружности, то точки B
, P
, Q
и N
принадлежат одной окружности и точки Q
, C
, M
и P
также принадлежат одной окружности. Используя этот факт, докажите, что \angle BQN=\angle CQM
.
Решение. Пусть дана точка P
, принадлежащая дуге BC
. Достаточно доказать, что \angle BQN=\angle CQM
.
Точки B
, P
, Q
и N
принадлежат одной окружности, так как
\angle BNP=\angle BQP=60^{\circ}.
Поэтому \angle BQN=\angle BPN
.
Точки Q
, C
, M
и P
также принадлежат одной окружности, так как
\angle QCM+\angle QMP=120^{\circ}+60^{\circ}=180^{\circ}.
Поэтому \angle CQM=\angle CPM
.
Поскольку
\angle BPC=\angle NPM=120^{\circ},
то \angle BPN=\angle CPM
. Следовательно, \angle BQN=\angle CQM
.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 51, с. 15
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 435, с. 52
